Nama :Bayu cahyadi
Kelas:TK 19 A
Npm :19316085
Distribusi Normal
A. Pengertian Distribusi Normal
Salah satu distribusi frekuensi yang paling penting dalam statistika adalah distribusi normal. Distribusi normal berupa kurva berbentuk lonceng setangkup yang melebar tak berhingga pada kedua arah positif dan negatifnya. Penggunaanya sama dengan penggunaan kurva distribusi lainnya. Frekuensi relatif suatu variabel yang mengambil nilai antara dua titik pada sumbu datar. Tidak semua distribusi berbentuk lonceng setangkup merupakan distribusi normal.
Pada tahun 1733 DeMoivre menemukan persamaan matematika kurva normal yang menjadi dasar banyak teori statistika induktif. Distribusi normal sering pula disebut Distribusi Gauss untuk menghormati Gauss (1777 – 1855), yang juga menemukan persamaannya waktu meneliti galat dalam pengukuran yang berulang-ulang mengenai bahan yang sama.
Distribusi normal, sering disebut puladistribusi Gauss, adalah distribusi probabilitas yang paling banyak digunakan dalam berbagai analisisstatistika. Distribusi normal bakuadalah distribusi normal yang memilikirata-rata nol dan simpangan baku satu. Distribusi ini juga dijuluki kurva lonceng(bell curve) karena grafik fungsi kepekatan probabilitasnya mirip dengan bentuk lonceng.
Distribusi normal memodelkan fenomena kuantitatif pada ilmu alammaupun ilmu sosial. Beragam skor pengujian psikologi dan fenomenafisika seperti jumlah foton dapat dihitung melalui pendekatan dengan mengikuti distribusi normal. Distribusi normal banyak digunakan dalam berbagai bidang statistika, misalnyadistribusi sampling rata-rata akan mendekati normal, meski distribusi populasi yang diambil tidak berdistribusi normal. Distribusi normal juga banyak digunakan dalam berbagai distribusi dalam statistika, dan kebanyakan pengujian hipotesismengasumsikan normalitas suatu data.
B. Sejarah Distribusi Normal
Distribusi normal pertama kali diperkenalkan oleh Abraham de Moivre dalamartikelnya pada tahun 1733 sebagai pendekatan distribusi binomial untuk n besar. Karyatersebut dikembangkan lebih lanjut oleh Pierre Simon de Laplace, dan dikenal sebagaiteorema Moivre-Laplace. Laplace menggunakan distribusi normal untuk analisis galat suatueksperimen. Metode kuadrat terkecil diperkenalkan oleh Legendre pada tahun 1805.Sementara itu Gauss mengklaim telah menggunakan metode tersebut sejak tahun 1794dengan mengasumsikan galatnya memiliki distribusi normal.
Istilah kurva loncengdiperkenalkan oleh Jouffret pada tahun 1872 untuk distribusi normal bivariat. Sementara ituistilah distribusi normal secara terpisah diperkenalkan oleh Charles S. Peirce, Francis Galton,dan Wilhelm Lexis sekitar tahun 1875. Terminologi ini secara tidak sengaja memiliki namasama.
C. Ciri Ciri Distribusi Normal
1. Memiliki parameter µ dan σ yang masing masing menentukan lokasi dan bentuk Distribusi
2. Kurvanya mempunyai puncak tunggal
3. Rata-rata terletak di tengah distribusi dan distribusinya simetris di sekitar garis tegaklurus yang ditarik melalui rata-rata
4. Total luas daerah di bawah kurva normal adala 1 (hal ini berlaku untuk seluruhdistribuso probabilitas kontinu
5. Kedua ekor kurva memanjang tak berbatas dan pernah memotong sumbu horizontal
6. Kurvanya berbentuk seperti lonceng atau genta
7. Simpangan baku atau standar deviasi σ menentukan lebarnya kurva. Makin kecil σ bentuk kurva semakin runcing.
D. Sifat-sifat penting distribusi normal adalah sebagai berikut:
1. Grafiknya selalu berada di atas sumbu x
2. Bentuknya simetris pada x = µ
3. Mempunyai satu buah modus, yaitu pada x = µ
4. Luas grafiknya sama dengan satu unit persegi, dengan rincian
a. Kira-kira 68% luasnya berada di antara daerah µ – σ dan µ + σ
b. Kira-kira 95% luasnya berada di antara daerah µ – 2σ dan µ + 2σ
c. Kira-kira 99% luasnya berada di antara daerah µ – 3σ dan µ + 3σ
Membuat kurva normal umum bukanlah suatu pekerjaan yang mudah. Lihat saja rumus untuk mencari fungsi densitasnya (nilai pada sumbu Y) begitu rumit. Oleh karena itu, orang tidak banyak menggunakannya.
Orang lebih banyak menggunakan DISTIBUSI NORMAL BAKU. Kurva distribusi normal baku diperoleh dari distribusi normal umum dengan cara transformasi nilai x menjadi nilai z, dengan formula sbb:
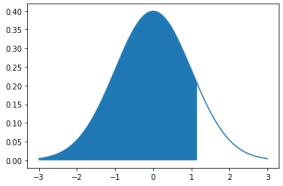
Kurva distribusi normal baku disajikan pada Gambar 2 berikut ini.
Gambar 2. Kurva distribusi normal baku
Kurva distribusi normal baku lebih sederhana dibanding kurva normal umum. Pada kurva distribusi normal baku, nilai µ = 0 dan nilai σ=1, sehingga terlihat lebih menyenangkan. Namun, sifat-sifatnya persis sama dengan sifat-sifat distribusi normal umum.
Untuk keperluan praktis, para ahli statistika telah menyusun Tabel distribusi normal baku dan tabel tersebut dapat ditemukan hampir di semua buku teks Statistika. Tabel distribusi normal bakui disebut juga dengan Tabel Z dan dapat digunakan untuk mencari peluang di bawah kurva normal secara umum, asal saja nilai µ dan σ diketahui. Sebagai catatan nilai µ dan σ dapat diganti masing-masing dengan nilai clip_image002 dan S.
E. Karakteristik Distribusi Normal
Suatu distribusi data dikatakan berdistribusi normal apabila data berdistribusi simetris, yaitu bila nilai rata-rata, median dan modus sama. Karakteristik distribusi normal antara lain:
1. Grafiknya akan selalu di atas sumbu datar x
2. Bentuk grafiknya simetris terhadap x = μ.
3. Mempunyai satu modus (unimodal)
4. Grafiknya mendekati (berasimptot) sumbu datar x
5. Luas daerah di bawah kurva adalah 1; ½ di sisi kanan nilai tengah dan ½ di sisi kiri.
F. Jenis-Jenis Distribusi Normal :
o Distribusi kurva normal dengan m sama dan s berbedao Distribusi kurva normal dengan m berbeda dan s samao Distribusi kurva normal dengan m dan s berbedao Luas di Bawah Kurva dan Probabilitas
Sebuah kurva normal, sangat penting dalam menghitung peluang sebab daerah yang ada dalam kurva tersebut menunjukkan besarnya peluang.
Dalam kajian statistika, luas daerah yang menunjukkan besarnya peluang itu disusun dalam sebuah daftar (tabel). Daftar (tabel) tersebut adalah daftar (tabel) distribusi normal baku (standar).
P (x1 < x < x2 ) = probabilitas variable random x memiliki nilai antara x1dan x2
P(x1 < x < x2) = luas di bawah kurva normal antara x = x1 dan x = x2
Oleh karena perhitungan integral normal tersebut sulit, maka disusunlah daftar (tabel) nilai rapat probabilitas. Akan tetapi karena nilai rapat probabilitasnya tergantung pada μ dan σ maka sangatlah tidak mungkin mentabelkan untuk semua nilai μ dan σ.
Kurva DIstribusi Normal Standard
Seperti diketahui, distribusi normal baku (standar) adalah distribusi normal dengan mean μ = 0 dan standard deviasi σ = 1.
Transformasi 〖Z= 〗^((X- μ)/σ) memetakan distribusi normal
Menjadi distribusi normal baku (standar), sebab distribusi normal dengan variabel z ini memiliki mean = 0 dan standar deviasi = 1.
Transformasi ini juga mempertahankan luas di bawah kurvanya, artinya:
Luas dibawah kurva distribusi normal antara x1 dan x2 sama dengan Luas dibawah kurva distribusi normal standard antara z1 dan z2
〖z1= 〗^(((x1- μ))/σ) Dan 〖z2=〗^(((x2- μ))/σ)
Sehingga cukup di buat tabel distribusi normal baku (standard) kumulatif saja.
Mencari Luas Di Bawah Kurva Normal
Untuk mempermudah dalam mencari luas di bawah kurva normal, perlu diperhatikan beberapa hal berikut :
Hitung luas z hingga dua desimal, misal z = 0,18
Gambarkan kurvanya
Letakkan harga z pada sumbu datar, lalu tarik garis vertikal hingga memotong kurva.
Luas daerah yang tertera dalam daftar adalah daerah antara garis vertikal yang ditarik dari titik harga z tadi dengan garis tegak di titik nol.
Dalam daftar distribusi normal baku, harga z pada kolom paling kiri hanya memuat satu desimal dan desimal kedua dicari pada baris paling atas.
Dari z kolom paling kiri, maju ke kanan dan dari z pada baris paling atas turun ke bawah, maka diperoleh bilangan yang merupakan daerah yang dicari (biasanya ditulis dalam empat desimal).
Karena luas seluruh kurva adalah satu satuan luas persegi, dan kurva simetris di titik 0, maka luas dari garis tegak pada titik nol ke kiri ataupun ke kanan adalah 0,5 satuan luas.
G. Kelebihan dan Kelemahan Distribusi Normal
Metode yang juga dikenal dengan sebutan forceddistribution ini mendapatkan namanya dari kenyataan bahwa para penilai yang terlibat memang “dipaksa” untuk mendistribusikan nilai karyawan ke dalam sejumlah kategori kinerja yang sudah ditetapkan persentase proporsinya. Biasanya, bentuk distribusi yang diterapkan adalah distribusi normal, dimana persentase yang setara kecilnya ditempatkan di kutub kanan (terbaik) dan kutub kiri (terburuk) sedangkan persentase yang lebih besar ditempatkan di bagian tengah — di antara kedua kutub tersebut.
Ø Kelebihan dari Distribusi Normal
1. Mengurangi kemungkinan terjadinya bias penilaian.
Dengan memaksa penilai untuk mendistribusikan hasil penilaiannya.
2. Meningkatkan objektivitas penilaian.
Karena harus memastikan penempatan setiap karyawan dalam suatu kategori, pada metode distribusi normal, para penilai perlu mengevaluasi semua karyawan berdasarkan kriteria yang sama.
3. Memfasilitasi terjadinya komunikasi yang spontan dan terbuka antara atasan dan bawahan.
Metode ini menuntut para atasan untuk secara berkala memberikan umpan balik kepada anak buah mereka. Tanpa kesediaan untuk sering menyampaikan umpan balik secara spontan dan terbuka.
Ø Kelemahan dari Distribusi Normal
1. Ketika diterapkan secara konsisten, metode distribusi normal justru membangkitkan tantangan baru yang menyulitkan.
Karena mengharuskan perusahaan untuk memecat karyawan yang dinilai berkinerja paling rendah, setelah diimplementasikan selama beberapa tahun, metode ini justru semakin mempersulit upaya membedakan karyawan yang berkinerja memuaskan dengan karyawan yang berkinerja istimewa.
2. Kategori yang digunakan tidak menunjukkan kinerja yang sebenarnya.
Pemaksaan nilai dan pengkategorian yang dipersyaratkan dalam metode distribusi normal membuat karyawan diberi nilai dan ditempatkan di kategori yang belum tentu sesuai dengan tingkat kinerja aktual mereka. Perusahaan yang berhasil mencapai target bisnisnya, misalnya, dimana semua karyawannya memang berprestasi bagus dan berhasil mencapai target mereka.
3. Terlalu memaksakan perbandingan kinerja antar-jabatan dalam upaya mendapatkan peringkat kinerja seluruh karyawan.
Pertanyaannya adalah: Bagaimana Anda akan secara fair dan objektif membandingkan kinerja seorang kepala departemen dengan kinerja seorang petugas administrasi? Atau kinerja Kepala Departemen Pemasaran dengan Kepala Departemen SDM? pertanyaan ini jelas mengusik rasa keadilan para pengemban jabatan yang diperbandingkan.
Contoh Soal :
Sebuah perusahaan bola lampu pijar mengetahui bahwa umur lampunya (sebelum putus) terdistribusi secara normal dengan rata-rata umurnya 800 jam dan standar deviasinya 40 jam. Carilah probabilitas bahwa sebuah bolam produksinya akan:
a. Berumur antara 778 jam dan 834 jam
b. Berumur kurang dari750 jam atau lebih dari 900 jam
Penyelesaian :
Diketahui : μ=800 dan σ=40
a. Berumur antara 778 jam 843 jam
P(778 < x < 843)
x1 = 778 → z_1 = [x_(1- μ)/σ] = [(778-800)/40] = -0,55
x2 = 843 → z_2 = [x_(2- μ)/σ] = [(843-800)/40] = 0,85
P (778 < x < 843) = P( - 0,55 < z < 0,85)
= P(z < 0,85) – P(z < - 0.55)
= 0,3022 – 0,2088 = 0,0934
b. Berumur kurang dari 750 jam atau lebih dari 900 jam
P(x < 750 atau x > 900)
x1 = 750 → z1 = [x_(1- μ)/σ] = [(750-800)/40] = -1,25
x2 = 900 → z2 = [z_(2- μ)/σ] = [(900-800)/40] = 2,5
P(x < 750 atau > 900) = P(z < - 1,25 ) + P (z > 2,5)
= P(z < -1,25) + 1 – P(z < 2,5)
= 1 + P(z < -1,25) – P(z < 2,5)
= 1 + 0,3944 – 0,4798 = 0,9146